资料分析中,大家学完之后的一个整体感受是感觉学的差不多了,但是可能对知识点的实质理解的还不是很到位,所以没办法将知识点迁移到其他题目里边灵活运用,不过没关系,我们一一的来攻克这些重点内容。
接下来主要给大家介绍一下比值比较问题。
一、比重比较是基础
其实比值比较问题的知识点是从比重比较知识点里拓展而来的,所以在系统的学习比值比较的知识点之前,我们先来把比重比较的内容回顾一下。
【引例】已知2018年,部分值为A,部分值的同比增长率为a%;整体值为B,整体值的同比增长率为b%,则A占B的比重与去年相比( )。
A.上升 B. 下降
解析:根据题意可判定本题为两期比重比较的知识点,不难得出两期比重:
现期比重=![]() ;
;
基期比重=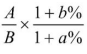 ;
;
现期比重-基期比重=![]() ;整个式子的正负只取决于a%-b%,若a%>b%,则现期比重-基期比重>0,即比重上升;若a%<b%,则现期比重-基期比重<0,即比重下降;以后判断比重上升下降,只需要找部分值和整体值的增长率,比大小得结果即可。
;整个式子的正负只取决于a%-b%,若a%>b%,则现期比重-基期比重>0,即比重上升;若a%<b%,则现期比重-基期比重<0,即比重下降;以后判断比重上升下降,只需要找部分值和整体值的增长率,比大小得结果即可。
这个结论是通过公式一步步推到出来的,接下来看一下这个结论背后的实质,如果我们把比重=![]() 的式子简单看成比值形式的话,则A为比值中的分子,那么a%不仅代表部分值的增长率,其实还代表了分子的增长率;同理b%为分母增长率,则结论可以演变为:当分子增长率(a%)>分母增长率(b%)时,比值上升;反之比值下降。为什么可以这么理解呢?这是基于分数性质,在
的式子简单看成比值形式的话,则A为比值中的分子,那么a%不仅代表部分值的增长率,其实还代表了分子的增长率;同理b%为分母增长率,则结论可以演变为:当分子增长率(a%)>分母增长率(b%)时,比值上升;反之比值下降。为什么可以这么理解呢?这是基于分数性质,在![]() 中,当分子增长速度大于分母时,即分子增长更快,则比值上升。所以以后遇到两期比值比较问题,则可以直接看分子与分母增速的大小得结果。
中,当分子增长速度大于分母时,即分子增长更快,则比值上升。所以以后遇到两期比值比较问题,则可以直接看分子与分母增速的大小得结果。
二、例题精讲
【例1】2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,增速比上半年放缓0.7个百分点。其中,工业品物流总额16636.15亿元,同比增长0.2%,增速比上半年放缓2.1个百分点;外部流入(含进口)货物物流总额17357.31亿元,同比增长12.1%,增速比上半年加快0.8个百分点;农产品物流总额8756亿元,同比增长11.6%,增速比上半年加快0.5个百分点;单位与居民物品物流总额457.86亿元,同比增长40.7%,增速比上半年放缓3个百分点;再生资源物流总额30.88亿元,同比下降7%,降幅比上半年扩大4.3个百分点。
在工业品物流、外部流入(含进口)货物物流、农产品物流、单位与居民物品物流和再生资源物流中,2018年的前三季度物流总额占社会物流总额的比重高于上年水平的有几类?
A.1 B.2
C.3 D.4
【答案】C
【解析】本题考查两期比重比较。
定位数据可知“2018年前三季度,S省社会物流额35357.26亿元,同比增长6.4%……工业品物流总额同比增长0.2%、外部流入(含进口)同比增长12.1%、农产品物流同比增长11.6%、单位与居民物品物流同比增长40.7%、再生资源物流同比下降7%”。
根据两期比重比较口诀“部分增长率高于整体,比重上升;反之,比重下降”,整体增长率为6.4%,有3个部分的增长率(12.1%、11.6%、40.7%)高于整体增长率,故有3个部分占整体的比重高于上年水平。因此,选择C选项。
【例2】2015年,纺织行业规模以上企业累计实现主营业务收入70713亿元,同比增长5%;实现利润总额3860亿元,同比增长5.4%;企业亏损面(亏损企业占所有企业比重)11.4%,比上年低0.1个百分点。
2015年,纺织行业规模以上企业主营业务收入利润率(利润总额/主营业务收入)比上年约:
A.上升 B.下降
【答案】A
【解析】本题考查两期利润率比较。
定位数据,“2015,纺织行业规模以上企业累计实现主营业务收入70713亿元,同比增长5%;实现利润总额3860亿元,同比增长5.4%”。根据两期利润率比较口诀,利润增长率大于收入增长率,则利润率上升,反之,利润率下降。代入数据a=5.4%>b=5%,利润率上升。因此,选择A选项。
【例3】2018年前三季度,S省社会物流总额35357.26亿元,同比增长6.4%,增速比上半年放缓0.7个百分点。2018年前三季度,S省社会物流总费用2682.1亿元,同比增长6.3%,比上半年放缓0.9个百分点,其中:物流运输环节总费用1854.6亿元,同比增长6.3%;保管环节总费用612.4亿元,同比增长6.4%;管理环节总费用214.9亿元,同比增长6.4%。
2018年前三季度,平均每万元社会物流总额产生的物流费用比上年同期:
A. 下降 B. 上升
【答案】A
【解析】本题考查两期平均数的比较问题。
定位数据,“2018年前三季度,S省社会物流额35357.26亿元,同比增长6.4%”,定位数据“2018年前三季度,S省社会物流总费用2682.1亿元,同比增长6.3%”。
根据平均数=后÷前,物流费用的增长率为a%,物流额的增长率为b%,代入数据a=6.3%<b=6.4%
因此,选择A选项。
三、总结
常见的比值形式分为两类,第一类代表比重,如利润率![]() (实际上求利润率即求利润占收入的比重)、资助率=
(实际上求利润率即求利润占收入的比重)、资助率=![]() 、产销比=
、产销比=![]() 、合格率、通过率等;第二类为非比重,如平均数、倍数等;
、合格率、通过率等;第二类为非比重,如平均数、倍数等;
通过以上几道例题的感知,不难发现,只要为![]() 这种形式,判断两期比值上升下降的问题,以后不用纠结比值中A和B的具体含义,直接找二者增长率比大小即可。
这种形式,判断两期比值上升下降的问题,以后不用纠结比值中A和B的具体含义,直接找二者增长率比大小即可。
资料分析的技巧很强,我们一起来深入研究吧!











